Laws of Illumination – Explanation, Formulas and Applications
Laws of Illumination – Explanation, Formulas and Applications
Illumination refers to the amount of light falling on a surface. Two important mathematical laws describe how illumination decreases with distance from a light source. Understanding these fundamental illumination principles is key for lighting design, computer graphics, photography, and more.
What is Illumination?
Before diving into the specific laws, let’s review some illumination basics.
Definition and Overview
Illumination describes how much light arrives at a point on a surface. It is measured in lux (lumens per square meter) or footcandles (lumens per square foot). The illuminance depends on factors like the light source intensity, distance, and angles.
Basic Principles and Terminology
Some key terms:
- Luminous flux: Total light output of the source, measured in lumens
- Intensity: Light output per unit solid angle, measured in candela
- Illuminance: Light arriving at a surface, measured in lux
Illumination obeys an inverse square relationship with distance from the source. It also varies by the angle of incidence of light striking a surface.
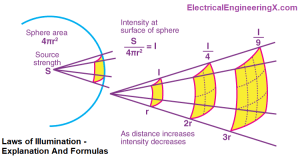
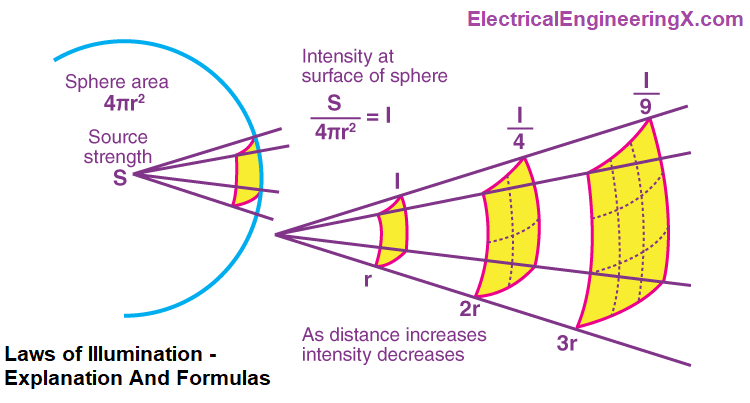
The Inverse Square Law of Illuminance
This fundamental law describes how illuminance decreases with distance.
Explanation of the Inverse Square Law
According to the inverse square law, illuminance decreases proportional to the inverse of the square of the distance from a point source.
Double the distance, and the illuminance decreases to 1/4. Triple the distance and it reduces to 1/9, and so on.
This happens because the same total light is spread over a larger area as distance increases.
Mathematical Formula
The formula is:
Illuminance = Intensity / (Distance)2
Where:
- Illuminance is measured in lux
- Intensity is in Candela
- Distance is measured from the source in meters
Practical Applications
Knowing illuminance levels is critical for proper lighting design. Some examples:
- General office lighting should be around 300-500 lux.
- Precision tasks like technical drawing require 1000-2000 lux.
- A darkened movie theater has an illuminance of around 10-50 lux.
The inverse square law lets designers calculate the required luminaire placement and intensity to achieve target lux levels.
The Cosine Law of Illuminance
While the inverse square law addresses distance, the cosine law describes the effect of angles.
Explanation of the Cosine Law
The cosine law says that illuminance decreases in proportion to the cosine of the angle between the light’s direction and the surface normal.
At normal incidence (0° angle), the cosine is 1, so illuminance is 100% of the initial value.
At a 60° angle, the cosine is 0.5, so illuminance is 50% of the initial maximum.
Mathematical Formula
Cosine law formula:
Illuminance = Emax * cos(theta)
Where:
- Emax is the maximum illuminance when light hits a perpendicular
- Theta is the angle between light and surface normal
Applications of the Cosine Law
Examples where the cosine law determines illumination:
- Time of day – The overhead midday sun gives higher illuminance than the low evening sun
- Light fixture placement – ceiling lights provide more illumination overhead than on vertical walls
- Reflectivity – matte surfaces reflect diffusely, losing illuminance at glancing angles
- Shadows – surfaces angled away from light source fall into shadow
Real-World Considerations for Illumination Laws
While ideal mathematical laws provide a starting point, real-world factors also affect illumination.
Reflectance and Surface Orientation
Reflectance characteristics of the surface alter reflected illuminance based on the viewing angle. A shiny surface reflects more light to the source than a matte, diffusely reflecting character.
Atmospheric Effects
Particles in the atmosphere can attenuate and scatter light during transmission, reducing illuminance levels with distance. Fog or haze has a significant effect.
Non-Point Light Sources
Formulas assume an ideal point source of light. Real fixtures have bulb shapes and sizes that affect illuminance at varying distances.
Calculation tools like ray-tracing software can account for many of these parameters. But often, some testing and calibration are still needed for final precision.
Uses and Importance of Illumination Laws
Now, let’s examine some important uses of these fundamental illumination principles.
Lighting Design and Installation
Lighting designers rely on the inverse square and cosine laws to determine required luminaire specifications, locations, beam angles, and mounting heights to provide target illuminance values on surfaces.
Computer Graphics and Visualization
CGI lighting models simulate real-world illumination behavior using the mathematical laws of illumination. This helps create ultra-realistic rendering and lighting effects.
Photography and Cinematography
Photographers consider inverse square and cosine principles for positioning lighting equipment and flash units. It helps achieve desired illumination aesthetics and practical exposure levels.
Conclusion and Summary
The illumination laws describe the inherent tradeoff between light source intensity and distance, and how surface angles alter perceived brightness. Mastering these foundational relationships allows true control and finesse over lighting across many fields like cinematography, architecture, computer animation, and more. Use this guide to understand the math and physics behind illumination deeply!
Frequently Asked Questions
Q: Does the inverse square law hold for non-point light sources?
A: No, real extended sources like lamps deviate from the inverse square law at close distances. But it is still a good approximation, especially at large distances.
Q: How quickly does illuminance decrease with distance?
A: According to the inverse square law, doubling the distance decreases illuminance to 1/4 the initial value. Illuminance drops rapidly as distance increases.
Q: What units are used to measure illuminance?
A: Illuminance is typically measured in lux (metric) or footcandles (imperial). One footcandle is approximately 10.76 lux.
Q: How can you increase low illuminance from a distant light?
A: Options include increasing the light source intensity, using reflectors to redirect light, using lower angle incidence, or decreasing distance if possible.
Q: Does atmospheric interference affect the inverse square law?
A: Yes, particles in the air scatter and absorb light during transmission, causing a faster-than-inverse-square drop-off with distance.
Q: Why does the sun provide less illuminance late in the day?
A: The lower sun angle means the sunlight strikes surfaces at an oblique angle rather than perpendicularly, reducing illuminance per the cosine law.
Q: How are lamp beam angles described mathematically?
A: Beam angles relate to solid angle measurements like steradians. The beam intensity profile follows a cosine law distribution.
Q: How do manufacturers specify luminaire intensities?
A: Intensities are typically specified by peak beam candela and by angle, such as “500-candela beam at 45 degrees.”
Q: What is the difference between illuminance and luminance?
A: Illuminance refers to light falling on a surface. Luminance describes the brightness of an illuminated surface or emitting source.
Q: Why are footcandles still used instead of lux in some applications?
A: Conventions are slow to change in some fields. Also, imperial units allow more fine gradations for illuminance values humans perceive.
MCQs
1. What is the practical significance of the Inverse Square Law of Illuminance?
This law helps designers and engineers determine how many light sources are needed and their placement to achieve the desired illumination level in a space.
2. How does the Cosine Law of Illuminance prevent over-illumination or shadows in architectural lighting?
By accounting for the angle of incidence, this law ensures that light is evenly distributed across a surface, preventing areas of excessive brightness or shadow.
3. Can I use the illuminance formulas for outdoor lighting design?
Yes, the illuminance formulas apply to outdoor lighting design, including street lighting and landscape illumination.
4. Are there specialized software tools for illuminance calculations in architectural design?
Yes, software tools are designed to calculate illuminance in architectural and lighting design projects.
5. Do the laws of illumination apply to natural lighting as well?
These laws apply to natural and artificial lighting, helping designers optimize natural light usage in buildings.
6. How do photographers use the laws of illumination in their work?
Photographers use these laws to control lighting conditions, create desired effects, and ensure proper photography exposure.
7. Are there international standards for illuminance levels in different settings?
Yes, organizations like the International Commission on Illumination (CIE) establish standards for illuminance levels in various environments, ensuring uniformity and safety.
8. Can the laws of illumination be applied to energy-efficient lighting design?
Understanding these laws is essential for designing energy-efficient lighting systems that minimize waste and optimize lighting quality.
9. Are there advancements in lighting technology that enhance the application of illuminance laws?
Yes, advancements in LED technology and intelligent lighting systems have expanded the possibilities for applying illuminance laws innovatively.